5.9 KiB
| title | date | tags | categories | mathjax | ||||
|---|---|---|---|---|---|---|---|---|
| Conception formelle : introduction | 2023-01-06 |
|
|
true |
Pourquoi?
Un peu d'histoire: les bugs célèbre
1985 : Banque de New-York
Un entier passe de 32768 à 0, conséquence : 2 jours d'interruption de service et 24 milliards de dollars d'emprunt et plus de 5 millions de perte.
1990: AT&T
Un break est oublié dans un case comme dans l'exemple ci-dessous:
switch(i) {
case 1 : function1(); break;
case 2 : function2(); // a forgotten break;
default: defaultfunction();
}
75 millions d'appels téléphonique dans le vide, pour American Airline, 200 000 réservations en moins. Heureusement AT&T utilisait déjà le réseau pour les déploiement. Si la propagation du bug a été accélérée, le déploiement du patch aussi.
1994 : bug du Pentium
Une erreur de calcul dans une fonction très particulière de processeur entrainait une erreur de calcul. La réponse d'Intel fut peu sympathique à l'époque qui assurait que peu de personnes utilisaient cette fonction etdonc qu'ils ne fixeraient pas le problème.
Depuis, Intel publie les preuves de calculs de leurs processeurs, tout comme AMD.
1996 : Ariane 5
Destruction de la fusée après 39 secondes de vol suite à deux grandes erreurs :
- conversion d'un entier 64 bits vers 16 bits avec overflow
- les deux ordinateurs utilisés pour la redondance partageaient le même code. Le bug était donc présent sur les deux machines.
1985 - 1987 : Thernac 25
Nous sommes ici en présence du premier bug ayant tué un humain. Le Thernac 25][l_thernac] était une machine utilisée en radiothérapie pour le traitement des cancers. Des patient se sont plaint de sensation de forte brulure lors de séances. Il a fallut attendre trois ans et au moins 4 morts pour que le fabricant rappelle ce modèle et mène l'investigation
Besoin de fiabilité
Dès les années 1990, il y a une prise de conscience générale de la nécessité de garanties pour le développement logiciel. Ce qui comprend ben entendu les test effectués sur le code, l'uniformisation de la sémantique utilisée(UML -- Universal Modelisation Laguage), les design patterns.
Panorama des méthodes formelles
Le but des méthodes formelles est de raisonner autour des logiciels pour déterminer les contrôles et comportements par les méthodes mathématiques.
Il faut pour cela obtenir un modèle former par l'analyse et le tester.
- est-ce que le modèle est le bon, est-il correct? : la validation
- pouvons nous vérifier le modèle? : la décidabilité[^n_decidabilite]
- pouvons nous traduire les résultats? : l'abstraction
[^n_decidabilite] ne proposition (on dit aussi énoncé) est dite décidable dans une théorie axiomatique si on peut la démontrer ou démontrer sa négation dans le cadre de cette théorie. Un énoncé mathématique est donc indécidable dans une théorie s'il est impossible de le déduire, ou de déduire sa négation, à partir des axiomes de cette théorie. Source Wikipedia
Pour qui?
Les méthodes coûtent cher et le personnel qualifié manque. Par conséquent seul les entreprises développant des systèmes complexes et/ou critiques les utilisent.
Quelques précisions :
- complexes : beaucoup d'interactions entre les composants
- critiques : important, que se soit économiquement, humainement ou les deux.
Les outils
L'idée derrière ce type d'outils: manipuler les preuves : un programme est un théorème, est-il adapté? C'estun autre problème.
Ces outils ne sont pas entièrement automatiques.
Interprération abstraite
Transformer une problème concret en un problème abstrait plus simple, rendant la preuve plus facile à produite
\( M_{\text{concret}} \models \phi \implies M_{\text{abstrait}} \models \phi \)
Vérification du modèle
Prendre en entrée un modèle \(M\), une spécification \(\phi\). ON vérifie alors que \(M\ \models \phi ).
Raffinement et implémentation
Autoriser la transformation d'une spécification en implémentation tout en préservant à chaque étapes les propriétés essentielles à notre système.
Gestion des tests
Génération de séquences de tests sur le modèle d'après la spécification. Ces tests dépendent du but recherchés.
Les test de conformités sont utilisés pour valider le vrai système. Les tests d'interopérabilité valident le système dans un contexte ouvert.
Système Stochastique
Utiliser les chaines de Markov et les [processus stochastique] l_stockas pour étudier la probabilité qu'un évènements se produise.
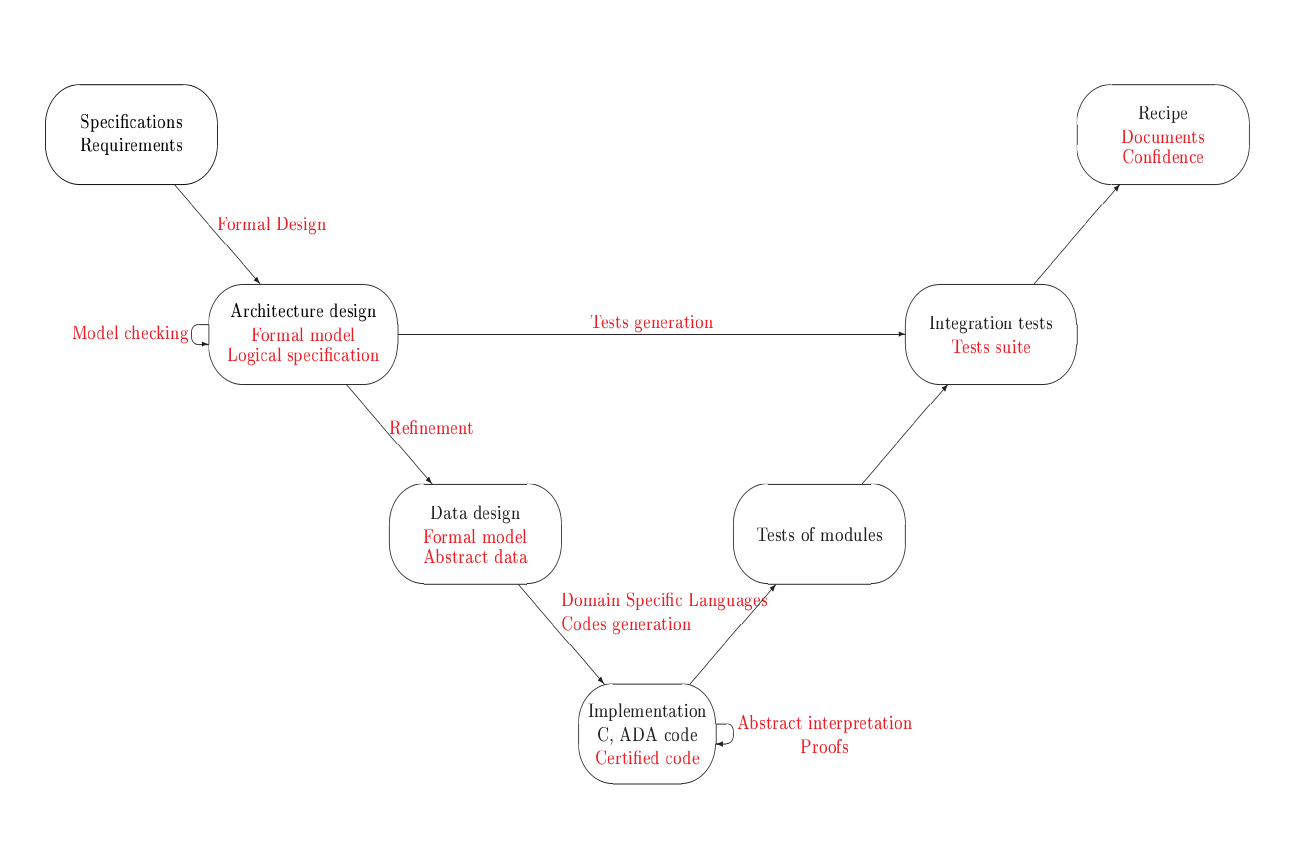
Choix de la méthode
Il n'y a pas une méthode à choisir, plusieurs méthodes formelles à appliquer en fonction de la position dans le cycle.
model checking
N'utilisons pas les données mais prouvons les interaction inter-modules :
- pour clarifier le cahier des charges
- pour aboutir un cahier des charges
Preuve de théorème
Ici nous validons l'algorithme afin de prouver qu'il fonctionne. Nous pouvons alors implémenter soir dans un langage généraliste, soir dans un langage dédié (donc spécifique). On obtient alors un code certifié.
Analyse de code binaire
Obtenir des garanties sur le code binaire -- qu'ils ne perturbent pas le système -- sans pour autant avoir le code source.
code source -> décompilation -> modèle -> analyse
Génération de tests
Génération de tests pertinents pour notre application partir du modèle et du cahier des charges.